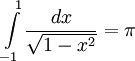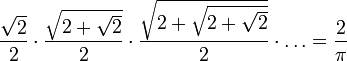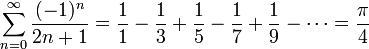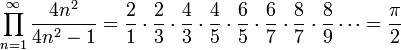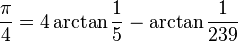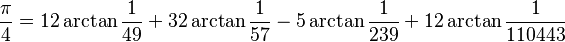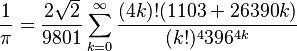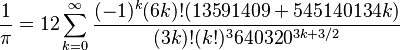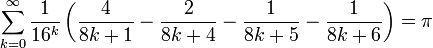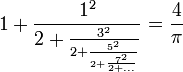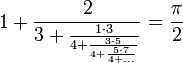Poznaj liczbe PI - Wzory do obliczen

Wzory do obliczania liczby Pi.

Powierzchnia koła jednostkowego:

$2cdotintlimits_{-1}^{ 1} sqrt{1-x^2},dx = pi$

Obwód okręgu jednostkowego:

$intlimits_{-1}^{ 1}frac{dx}{sqrt{1-x^2}} = pi$

François Viète, 1593:

$frac{sqrt2}2 cdot frac{sqrt{2+sqrt2}}2 cdot frac{sqrt{2+sqrt{2+sqrt2}}}2 cdot ldots = frac2pi$

Leibniz:

$sum_{n=0}^{infty} frac{(-1)^{n}}{2n+1} = frac{1}{1} - frac{1}{3} + frac{1}{5} - frac{1}{7} + frac{1}{9} - cdots = frac{pi}{4}$

Wallis:

$prod_{n=1}^{infty} frac{4n^2}{4n^2-1} = frac{2}{1} cdot frac{2}{3} cdot frac{4}{3} cdot frac{4}{5} cdot frac{6}{5} cdot frac{6}{7} cdot frac{8}{7} cdot frac{8}{9} cdots = frac{pi}{2}$

Powyższe metody są wolno zbieżne. Do szybkich obliczeń komputerowych stosuje się przybliżenie wynikające z tożsamości:

$frac{pi}{4} = 4 arctanfrac{1}{5} - arctanfrac{1}{239}$

Funkcję arcus tangens należy rozwinąć w szereg Taylora. Twórcą tej formuły jest angielski matematyk John Machin (1680—1751).

Szybkozbieżnych formuł postaci :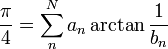 $frac{pi}{4} = sum_{n}^N a_n arctanfrac{1}{b_n}$ pojawiło się więcej, m.in:

K. Takano (1982):

$frac{pi}{4} = 12 arctanfrac{1}{49} + 32 arctanfrac{1}{57} - 5 arctanfrac{1}{239} + 12 arctanfrac{1}{110443}$

F. C. W. Störmer (1896):

$frac{pi}{4} = 44 arctanfrac{1}{57} + 7 arctanfrac{1}{239} - 12 arctanfrac{1}{682} + 24 arctanfrac{1}{12943}$

S. Klingenstierna (1730):

$frac{pi}{4} = 8 arctanfrac{1}{10} - arctanfrac{1}{239} - 4 arctanfrac{1}{515}$

Inne metody:

Newton:

$frac{pi}{2}= sum_{k=0}^inftyfrac{k!}{(2k+1)!!}= 1+frac{1}{3}left(1+frac{2}{5}left(1+frac{3}{7}left(1+frac{4}{9}(1+...)right)right)right)$

Ramanujan:

$frac{1}{pi} = frac{2sqrt{2}}{9801} sum^infty_{k=0} frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}$

David Chudnovsky i Gregory Chudnovsky:

$frac{1}{pi} = 12 sum^infty_{k=0} frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}$

Bailey-Borwein-Plouffe Bailey web page (1997)

$sum_{k=0}^inftyfrac{1}{16^k}left(frac {4}{8k+1} - frac {2}{8k+4} - frac {1}{8k+5} - frac {1}{8k+6}right) = pi$

Istnieją także rozwinięcia w ułamki łańcuchowe:

W. Brouncker (ok. 1600)

$1+frac{1^2}{2+frac{3^2}{2+frac{5^2}{2+frac{7^2}{2+...}}}}=frac{4}{pi}$

L. Euler (ok. 1755)

$1+frac{2}{3+frac{1cdot 3}{4+frac{3cdot 5}{4+frac{5cdot 7}{4+...}}}}=frac{pi}{2}$

Nadaj zmiennej a wartość 3

Nadaj zmiennej b wartość 3

Nadaj zmiennej s wartość sqrt(3)/2 (Sinus kata Pi/a)

Nadaj zmiennej t wartość sqrt(3) (Tangens kąta Pi/b)

Dopóki wartość bezwzględna z różnicy s i t jest większa od zadanej dokładności to

Nadaj zmiennej a jej podwojona wartość

Nadaj zmiennej b jej podwojona wartość

Nadaj zmiennej s wartość sinusa połówkowego

Nadaj zmiennej t wartość tangensa połówkowego

Pi leży w przedziale [as;bt]