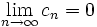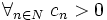Liczba π jest liczbą niewymierną, co oznacza, że nie może być zapisana jako iloraz dwóch liczb całkowitych. Udowodnił to w roku 1761 Johann Heinrich Lambert. Co więcej, jest ona liczbą przestępną, co w 1882 roku wykazał Ferdinand Lindemann. Oznacza to, że nie istnieje wielomian o współczynnikach całkowitych, którego π jest pierwiastkiem. W rezultacie nie jest możliwe zapisanie π za pomocą skończonego zapisu złożonego z liczb całkowitych, działań arytmetycznych, ułamków oraz potęg i pierwiastków.

Przybliżona konstrukcja Kochańskiego:

To ostatecznie rozstrzyga, że niemożliwa jest klasyczna konstrukcja (wyłącznie przy pomocy linijki i cyrkla) kwadratu o powierzchni równej powierzchni danego koła, gdyż współrzędne wszystkich punktów, które mogą być skonstruowane w taki sposób, należą do zbioru liczb nazywanych liczbami algebraicznymi. Problem ten zwany jest kwadraturą koła i choć nie ma on ścisłego rozwiązania, to istnieją konstrukcje przybliżone. Powiązanym, również niemożliwym do rozwiązania problemem, jest problem rektyfikacji okręgu, do którego również istnieją konstrukcje przybliżone, z których za jedną z najprostszych uchodzi konstrukcja Adama Adamandego Kochańskiego.

Dowód niewymierności π

Dowód przez sprowadzenie do sprzeczności.

Zakładamy, że 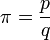gdzie .

Ustalamy ciąg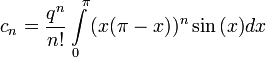

Można wykazać, że:

Oznaczać to będzie, że przyjęte założenie 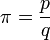prowadzi do sprzeczności, gdyż ciąg liczb całkowitychdodatnich nie może być zbieżny do liczby 0.